6
Classification
Classification is one of the most widely used data mining techniques. In very general terms, given a list of groups (often called classes ), classification seeks to predict which group a new instance may belong to. The outcome of classification is typically either to identify a single group or to produce a probability distribution of the likelihood of membership for each group. It is the most important case of supervised learning, meaning that the labels available to the learning algorithm can be used to guide it. A spam filter is a good example, where we want to predict whether new emails are considered spam or not. Twitter sentiment analysis is another example, where we want to predict whether the sentiment of a new incoming tweet is positive or negative.
More formally, the classification problem can be formulated as follows: we are given a set of labeled instances or examples of the form ( x, y ), where x = x 1 , . . . , x k is a vector of feature or attribute values, and y is one of n C different classes , regarded also as the value of a discrete attribute called the class . The classifier building algorithm builds a classifier or model f such that y = f ( x ) is the predicted class value for any unlabeled example x . For example, x could be a tweet and y the polarity of its sentiment; or x could be an email message, and y the decision of whether it is spam or not. Most classic methods for classification load all training data into main memory and then build f via multiple passes over the data. In the stream setting, f is typically constructed incrementally, with inspection of data restricted to a single pass with instances presented one at a time.
We start by reviewing how to evaluate classifiers, the most popular classification methods, and how they can be applied in a data stream setting. The two important characteristics of any classification method in the stream setting are: that limitations exist in terms of memory and time (so that we cannot store all instances in memory), and that classification models must be able to adapt to possible changes in the distribution of the incoming data. These characteristics imply that exact solutions are unlikely, so we should expect approximate solutions and therefore expect the associated error to be bounded. Bounds on error are problematic in the sense that, when they themselves make few assumptions about the distribution generating the error, they tend to be conservative (that is, in practice, results are much better than predicted by the bound). When they do make assumptions, they can be much more consistent with experimental results, but are vulnerable to cases where those assumptions simply do not hold.
A third requirement, not covered in this chapter, is the ability to cope with changes in the feature space. In a sensor network, for example, it is likely that one or more sensors providing values to certain features will go offine now and then due to malfunction or replacement. The replacement sensors could be newer models, so they might make measurements differently from the past. In fact, it makes sense that a sensor could be removed permanently. Almost all stream classification algorithms assume that the feature space is fixed and cannot respond easily to this type of change. Aside from the feature space, the set of class labels could also change over time. Thus algorithms would need to be able to cope with the addition of new class labels and the deletion of existing ones. Both these changes in x and y represent fertile ground for the development of new stream classification algorithms.
6.1 Classifier Evaluation
Evaluation is one of the most fundamental tasks in all data mining processes, since it helps to decide which techniques are more appropriate for a specific problem, and to set parameters. The main challenge is to know when a method is outperforming another method only by chance, and when there is a statistical significance to that claim. Some of the methodologies applied in stream mining are the same as in the case of nonstreaming data, where all data can be stored in memory. However, mining data streams poses new challenges and must use modified evaluation methodologies.
One thing worth noting before we continue is that almost all the discoveries made in data mining, and particularly classification, assume that data is independently and identically distributed (IID). Thus a stationary distribution is randomly producing data in no particular order, and the underlying distribution generating the data is not changing. In a streaming environment no part of the IID assumption remains valid. It is often the case, for example, that for certain time periods the labels or classes of instances are correlated. In intrusion detection, there are long periods where all class labels are no-intrusion, mixed with infrequent, short periods of intrusion. This is another aspect of data stream mining that would benefit from further research.
An evaluation framework should be composed of the following parts:
- error estimation,
- evaluation performance measures,
- statistical significance validation, and
- a cost measure of the process.
For evolving data streams, the main difference from traditional data mining evaluation is how to perform the error estimation. Resources are limited and cross-validation may be too expensive. We start by looking at how to define and estimate accuracy, then we look at which measures are the most convenient to measure the performance of the algorithms. Finally we review some statistical techniques for checking significance and measuring the cost of the overall process.
6.1.1 Error Estimation
The evaluation procedure of a learning algorithm determines which examples are used for training the algorithm and which are used for testing the model output by the algorithm.
In traditional batch learning, a first approach is to split the dataset into disjoint training and test sets. If the data is limited, cross-validation is preferable: we create several models and average the results with different random arrangements of training and test data.
In the stream setting, (effectively) unlimited data poses different challenges. Cross-validation typically is computationally too expensive, and not as necessary. On the other hand, creating a picture of accuracy over time is essential. The following main approaches arise:
- Holdout: When data is so abundant that it is possible to have test sets periodically, then we can measure the performance on these holdout sets. There is a training data stream that is used to train the learner continuously, and small test datasets that are used to compute the performance periodically. In MOA, the implementation of this concept requires the user to specify two parameters (say, j and k ): j is the size of the first window (set of instances) for testing purposes, and k is the frequency of testing—that is, test after every k instances (using a test set of size j ).
- Interleaved test-then-train: Each individual example can be used to test the model before it is used for training, and from this, the accuracy can be incrementally updated. The model is thus always being tested on examples it has not seen. In MOA, this scheme is implemented using a landmark window model (data in the stream is considered from the beginning to now).
- Prequential: Like interleaved test-then-train but—in MOA—implements the idea that more recent examples are more important, using a sliding window or a decaying factor. The sizes of the sliding window and the decaying factor are parameters.
- Interleaved chunks: Also like interleaved test-then-train, but with chunks of data in sequence. Chunks of different sizes may need to be considered (this is a parameter in the MOA implementation).
Note that if we set the size of the sliding window to the number of instances in the entire dataset, then the middle two schemes are equivalent.
Holdout evaluation more accurately estimates the accuracy of the classifier on more recent data. However, it requires recent test data that is difficult to obtain for real datasets. There is also the issue of ensuring coverage of important change events: if the holdout is during a less volatile period of change, then it might overestimate classifier performance.
Gama et al. [ 115 ] propose a forgetting mechanism for estimating holdout accuracy using prequential accuracy: a sliding window of size w with the most recent observations, or fading factors that weigh observations using a decay factor α . The fading factor α is used as follows:
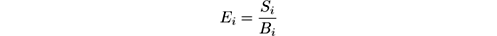
with

where n i is the number of examples used to compute the loss function L i . We have n i = 1 since the loss L i is computed for every single example.
The output of the two mechanisms is very similar, as a window of size w may be approximated by a decay factor α ∼ 1 /w . Figure 6.1 shows a comparison of a holdout evaluation, an interleaved test then train evaluation, and a prequential evaluation using a sliding window of size 1,000. Looking at the plot in figure 6.1 it seems that, at least for this dataset, prequential evaluation using a sliding window is a good approximation of holdout evaluation.
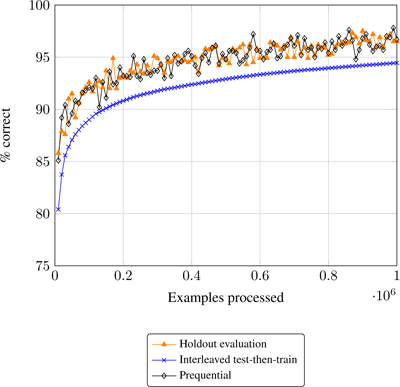
Figure 6.1
Evaluation on a stream of 1,000,000 instances, comparing holdout, interleaved test-then-train, and prequential with sliding window evaluation methods.
6.1.2 Distributed Evaluation
In a distributed data stream setting, we have classifiers that can be trained at the same time. This provides an opportunity to implement something akin to classic k -fold cross-validation. Several approaches to evaluation in this setting have been proposed to cover combinations of data abundance or scarcity, and numbers of classifiers to be compared [ 40 ]:
- k -fold distributed split-validation: when there is abundance of data and k classifiers. Each time a new instance arrives, it is decided with probability 1 /k whether it will be used for testing. If it is used for testing, it is used by all the classifiers. If not, then it is used for training and assigned to only one classifier. Thus, each classifier sees different instances, and they are tested using the same data.
- 5 x 2 distributed cross-validation: when data is less abundant, and we want to use only, say, ten classifiers. We create five groups of classifier pairs, and for each group, each time a new instance arrives, it is decided with probability 1/2 which of the two classifiers is used to test; the other classifier of the group is used to train. All instances are used to test or to train, and there is no overlap between test instances and train instances.
- k -fold distributed cross-validation: when data is scarce and we have k classifiers. Each time a new instance arrives, it is used for testing in one classifier selected at random, and for training in the others. This evaluation is equivalent to k -fold distributed cross-validation.
6.1.3 Performance Evaluation Measures
In real data streams, the number of instances for each class may be evolving and changing. It may be argued that the prequential accuracy measure is only appropriate when all classes are balanced and have approximately the same number of examples. The Kappa statistic is a more sensitive measure for quantifying the predictive performance of streaming classifiers.
The Kappa statistic κ was introduced by Cohen [ 76 ] and defined as follows:
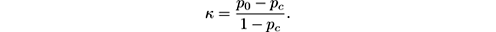
The quantity p 0 is the classifier’s prequential accuracy, and p c is the probability that a chance classifier—one that randomly assigns to each class the same number of examples as the classifier under consideration—makes a correct prediction. If the classifier is always correct, then κ = 1. If its predictions coincide with the correct ones as often as those of a chance classifier, then κ = 0.
The Kappa M statistic κ m [ 40 ] is a measure that compares against a majority class classifier instead of a chance classifier:
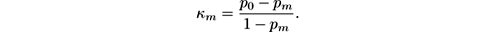
In cases where the distribution of predicted classes is substantially different from the distribution of the actual classes, a majority class classifier can perform better than a given classifier while the classifier has a positive κ statistic.
An alternative to the Kappa statistic is to compute the area under the receiver operating characteristics curve AUC. Brzezinski and Stefanowski present in [ 59 ] an incremental algorithm that uses a sorted tree structure with a sliding window to compute AUC with forgetting. The resulting evaluation measure is called prequential AUC, and is also available in MOA.
Another Kappa measure, the Kappa temporal statistic [ 42 , 262 ], considers the presence of temporal dependencies in data streams. It is defined as
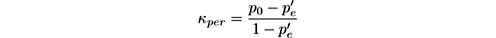
where
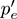 is the accuracy of the No-change classifier, the classifier that simply echoes the last label received (section 6.2.2), a simple and useful classifier when the same labels appear together in bursts.
is the accuracy of the No-change classifier, the classifier that simply echoes the last label received (section 6.2.2), a simple and useful classifier when the same labels appear together in bursts.
Statistic κ per takes values from 0 to 1. The interpretation is similar to that of κ : if the classifier is perfectly correct, then κ per = 1. If the classifier is achieving the same accuracy as the No-change classifier, then κ per = 0. Classifiers that outperform the No-change classifier fall between 0 and 1. Sometimes κ per < 0, which means that the classifier is performing worse than the No-change baseline.
Using κ per instead of κ m , we can detect misleading classifier performance for data that is not IID. For highly imbalanced but independently distributed data, the majority class classifier may beat the No-change classifier. The κ per and κ m measures can be seen as orthogonal, since they measure different aspects of the performance.
Other measures that focus on the imbalance among classes are the arithmetic mean and the geometric mean:

where A i is the testing accuracy on class i and n c is the number of classes. Note that the geometric accuracy of the majority vote classifier would be 0, as accuracy on the classes other than the majority would be 0. The accuracy of a perfectly correct classifier would be 1. If the accuracies of a classifier are equal for all classes, then both arithmetic and geometric accuracies are equal to the usual accuracy.
Consider the simple confusion matrix shown in table 6.1 . From this table, we see that Class+ is predicted correctly 75 times, and Class− is predicted correctly 10 times. So accuracy p 0 is 85%. However, a classifier predicting solely by chance—in the given proportions—will predict Class+ and Class− correctly in 68.06% and 3.06% of cases respectively. Hence, it has accuracy p c = 71.12% and κ = 0.48; the majority class classifier has accuracy p m = 75% and κ m = 0.40.
Table 6.1
Simple confusion matrix example.
|
Predicted |
Predicted |
||
|
Class+ |
Class− |
Total |
|
|
Correct Class+ |
75 |
8 |
83 |
|
Correct Class− |
7 |
10 |
17 |
|
Total |
82 |
18 |
100 |
The accuracy for Class+ is 90.36% and for Class− is 58.82%. The arithmetic mean A is 74.59%, and the geometric mean G is 72.90%. So we see that A ≥ G and that G tends to the lower value.
Imagine that, as shown in table 6.2 , the number of misclassified examples of Class− increases to 57. Then, the accuracy for Class− decreases to 14.92%, κ to 0.05, and κ m to 0.13. The arithmetic mean A changes to 52.64%, and the geometric mean G to 36.72 %.
Table 6.2
Confusion matrix of
table 6.1
, modified.
|
Predicted |
Predicted |
||
|
Class+ |
Class− |
Total |
|
|
Correct Class+ |
75 |
8 |
83 |
|
Correct Class− |
57 |
10 |
67 |
|
Total |
132 |
18 |
150 |
6.1.4 Statistical Significance
When evaluating classifiers, we should be concerned with the statistical significance of the results. Looking at the performance of only one classifier, it is convenient to give some insights about its statistical significance. We may use confidence intervals of parameter estimates to indicate the reliability of our estimate. To do that, we can use Chernoff’s or Hoeffding’s bounds, which are sharper than Markov’s or Chebyshev’s inequalities, because the measures we are interested in are averages of evaluations on individual items. For reasonably large numbers of points the approximation by a normal is usually applicable; see section 4.2.
When comparing two classifiers, we need to distinguish between random and nonrandom differences in the experimental accuracies. McNemar’s test [ 173 ] is the most popular nonparametric test in the stream mining literature to assess the statistical significance of differences in the performance of two classifiers. This test needs to store and update two variables: the number of instances misclassified by the first classifier and not by the second, a , and the number of instances misclassified by the second classifier and not by the first, b . The McNemar statistic is given as M = | a − b − 1| 2 /( a + b ). The test follows the χ 2 distribution. At 0.99 confidence it rejects the null hypothesis (the performances are equal) if M > 6.635.
Although the field of ML is several decades old, there is still much debate around the issue of comparing the performance of classifiers and, consequently, measurements of significant performance difference. The latest contribution is by Berrar [ 29 ], who argues that the magnitude of the difference in performance (and reasonable bounds on that difference) should be the focus, not statistical significance. The outcome of this work is a new evaluation tool called confidence curves, curves that show the magnitude difference directly. Issues with null hypothesis significance testing and p -values have also recently led to Bayesian alternatives to the problem being proposed [ 78 ]. Thus, it is not possible at this time to give a definitive answer to the question of performance measurement, as further research in classic and streaming ML is still needed. In particular, a measure for estimating the effect size over time for data streams has yet to be proposed.
6.1.5 A Cost Measure for the Mining Process
The issue of measuring three evaluation dimensions simultaneously has led to another important issue in data stream mining, namely, estimating the combined cost of performing the learning and prediction processes in terms of time and memory. As an example, several rental cost options exist:
- Cost per hour of usage: Amazon Elastic Compute Cloud (Amazon EC2) is a web service that provides resizable computing capacity in the cloud. The cost depends on the time and on the size of the machine rented (for example, small instance with 2 GB of RAM, large with 8 GB or extra large with 16 GB).
- Cost per hour and memory used: GoGrid is a web service similar to Amazon EC2, but it charges by RAM-hours. Every GB of RAM deployed for 1 hour equals by definition 1 RAM-hour.
The use of RAM-Hours as defined above was introduced in [ 37 ] as an evaluation measure of the resources used by streaming algorithms. Although proposed for learning, it can be applied to the other data mining tasks.
6.2 Baseline Classifiers
Batch learning has led to the development of hundreds of different classifiers that belong to a number of paradigms, such as divide-and-conquer methods, rule learners, lazy learners, kernel methods, graphical models, and so on. If we are to streamify methods from these paradigms, we need to consider how to make them both incremental and fast. Some methods are naturally incremental and fast, and we will start with these. Research on the application of batch methods to large datasets tells us to look for methods with good bias management. If a method has high bias, like the ones we will introduce next, then its ability to generalize will be limited. Methods producing more complex models are typically better at generalization but have necessarily higher maintenance costs and should be controlled for overfitting. Producing methods that manage the trade-off well (complexity of model representation versus speed of model update) is the main issue in data stream classification research.
6.2.1 Majority Class
The Majority Class algorithm is one of the simplest classifiers: it predicts the class of a new instance to be the most frequent class. It is used mostly as a baseline, but also as a default classifier at the leaves of decision trees. A Majority Class classifier is very easy to compute and maintain, as it only needs to keep an array of counters for each one of the classes.
6.2.2 No-change Classifier
Another simple classifier for data streams is the No-change classifier, which predicts the label for a new instance to be the true label of the previous instance. Like the Majority Class classifier, it does not require the instance features, so it is very easy to implement. In the intrusion detection case where long passages of “no intrusion” are followed with briefer periods of “intrusion,” this classifier makes mistakes only on the boundary cases, adjusting quickly to the consistent pattern of labels.
When a temporal dependence among consecutive labels is suspected, it usually pays to add the label(s) of the previous instance(s) as new attributes. This capability, proposed in [ 42 , 262 ], is available as a generic wrapper T EMPORALLY A UGMENTED C LASSIFIER in MOA.
6.2.3 Naive Bayes
Naive Bayes is a classification algorithm known for its low computational cost and simplicity. As an incremental algorithm, it is well suited for the data stream setting. However, it assumes independence of the attributes, and that might not be the case in many real data streams.
It is based on Bayes’ theorem, which may be stated informally as
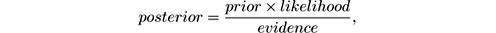
that is, it tells how the probability of an event is modified after accounting for evidence. More formally:
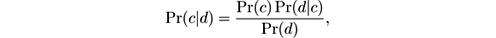
where Pr( c ) is the prior, the initial probability of event c , Pr( c | d ) is the posterior, the probability after accounting for d , Pr( d | c ) is the likelihood of event d given that event c occurs, and Pr( d ) is the probability of event d . It is based on the definition of conditional probability, by which Pr( c ∩ d ) = Pr( c )Pr( d | c ) = Pr( d )Pr( c | d ).
The Naive Bayes model is built as follows: Let x 1 , …, x k be k discrete attributes, and assume that x i can take n i different values. Let C be the class attribute, which can take n C different values. Upon receiving an unlabeled instance I = ( x 1 = v 1 ,… ,x k = v k ), the Naive Bayes classifier computes a “probability” of I being in class c as:
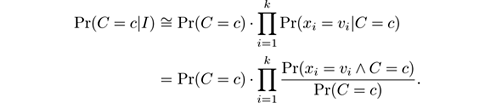
The values Pr( x i = v j ∧ C = c ) and Pr( C = c ) are estimated from the training data. Thus, the summary of the training data is simply a 3-dimensional table that stores for each triple ( x i ,v j ,c ) a count n i,j,c of training instances with x i = v j and class c , together with a 1-dimensional table for the counts of C = c . This algorithm is naturally incremental: upon receiving a new example (or a batch of new examples), simply increment the relevant counts. Predictions can be made at any time from the current counts.
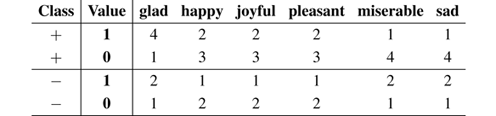
Example 6.1 Suppose we have the following dataset of tweets, and that we want to build a model to predict the polarity of newly arriving tweets.
|
ID |
Text |
Sentiment |
|
T1 |
glad happy glad |
+ |
|
T2 |
glad glad joyful |
+ |
|
T3 |
glad pleasant |
+ |
|
T4 |
miserable sad glad |
− |
First, we transform the text associated with each instance to a vector of attributes.
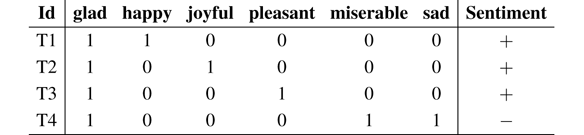
Now, we can build a table with the counts for each class:
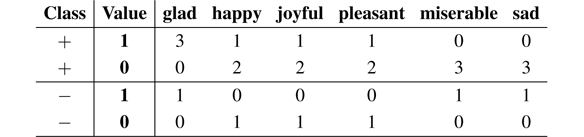
Assume we have to classify the following new instance:
|
ID |
Text |
Sentiment |
|
T5 |
glad sad miserable pleasant glad |
? |
First, we convert it to a vector of attributes.

And now we compute the probabilities as follows:
- Pr(+| T 5) = Pr(+) · Pr( glad = 1|+) · Pr( happy = 0|+) · Pr( joyful = 0|+) · Pr( pleasant = 1|+) · Pr( miserable = 1|+) · Pr( sad = 1|+), so
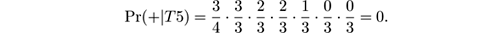
- Pr(−| T 5) = Pr (−) · Pr( glad = 1|−) · Pr( happy = 0|−) · Pr( joyful = 0|−) · Pr( pleasant = 1|−) · Pr( miserable = 1|−) · Pr( sad = 1|−), so
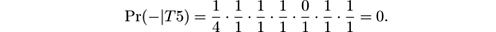
We see that the probabilities are equal to 0 the moment a single term is 0, which is too drastic. A way to avoid this is using the Laplace correction , which is adding, for example, 1 to the numerator and the number of classes to the denominator to allow for unseen instances:
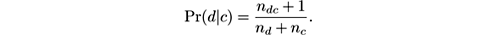
In practice, this is done by initializing the counters to 1. In our example, the table of counts for each class becomes:
And recomputing the probabilities we get:
- Pr(+| T 5) = Pr(+) · Pr( glad = 1|+) · Pr( happy = 0|+) · Pr( joyful = 0|+) · Pr( pleasant = 1|+) · Pr( miserable = 1|+) · Pr( sad = 1|+), so
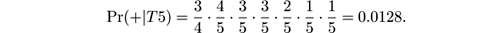
- Pr(−| T 5) = Pr(−) · Pr( glad = 1|−) · Pr( happy = 0|−) · Pr( joyful = 0|−) · Pr( pleasant = 1|−) · Pr( miserable = 1|−) · Pr( sad = 1|−), so
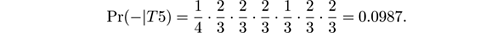
We see that Pr(−| T 5) > Pr(+| T 5) and the Naive Bayes classifier predicts that the new tweet has negative polarity.
Observe that the two probabilities do not add up to 1 as they should, because we have ignored the term Pr( d ) in Bayes’ theorem. It is normally impossible to assess the probability of a specific data point from a sample. We, can, however normalize by the sum to obtain figures that add up to 1.
6.2.4 Multinomial Naive Bayes
The Multinomial Naive Bayes classifier [ 171 ] is an extension of Naive Bayes for document classification that often yields surprisingly good results. Multinomial Naive Bayes considers a document as a bag of words, so it takes into account the frequency of each word in a document and not just its presence or absence. Since word frequency is usually relevant for text classification, this method is preferred over Naive Bayes for text mining.
Let n wd be the number of times word w occurs in document d . Then the probability of class c given a test document is calculated as follows:
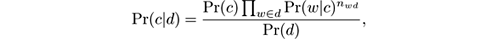
where Pr( d ) can be thought of as a normalization factor.
But a key difference with Naive Bayes is the interpretation of Pr( w | c ): here it is the ratio between the number of occurrences of w in documents of class c over the total number of words in documents of class c . In other words, it is the probability of observing word w at any position of a document belonging to class c . Observe that, again unlike Naive Bayes, the absence of a word in a document does not make any class more likely than any other, as it translates to a 0 exponent.
Conveniently, n wd , Pr( w | c ) and Pr( c ) are trivial to estimate on a data streams by keeping the appropriate counters. Laplace correction can be added by initializing all the counts to 1 instead of 0.
Example 6.2 Suppose we want to build a Multinomial Naive Bayes classifier using the tweets in example 6.1. First we compute the number of occurrences of each word in each document. We use Laplace correction, setting each entry to 1 before starting to count occurrences:

And now the probabilities for each class are:
-
Pr(+|
T
5) =
Pr(+) · Pr( glad |+) · Pr( pleasant |+) · Pr( miserable |+) · Pr( sad |+),
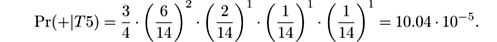
-
Pr(−|
T
5) =
Pr(−) · Pr( glad |−) · Pr( pleasant |−) · Pr( miserable |−) · Pr( sad |−),
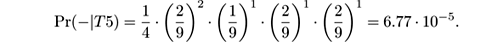
In this case, we see that Pr(+| T 5) > Pr(−| T 5) and the Multinomial Naive Bayes classifier predicts that the new tweet has positive polarity, in contrast to regular Naive Bayes, which predicted negative polarity.
6.3 Decision Trees
Decision trees are a very popular classifier technique since it is very easy to interpret and visualize the tree models. In a decision tree, each internal node corresponds to an attribute that splits into a branch for each attribute value, and leaves correspond to classification predictors, usually majority class classifiers. Figure 6.2 shows an example.
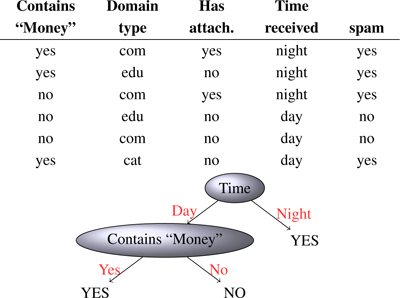
Figure 6.2
A dataset describing email features for deciding whether the email is spam, and a decision tree for it.
The accuracy of decision trees can be improved using other classifiers at the leaves, such as Naive Bayes, or using ensembles of decision trees, as we will see later on.
The basic method to build a tree is to start by creating a root node at the beginning node = root , and then do the following:
- If training instances are perfectly classified at the node, then stop. Else:
- Assign A to be the “best” decision attribute for node .
- For each value of A , create new descendant (leaf) of node .
- Split the training instances according to the value of A , and pass each split to the corresponding leaf.
- Apply this method recursively to each leaf.
Two common measures are used to select the best decision attribute:
-
Information gain, that is, the difference between the entropy of the class before and after splitting by the attribute. Recall that the entropy
H
of a sample
S
is
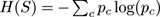 , where
p
c
is the probability in
S
of class label
c
. The entropy of
S
after splitting on attribute
A
is
, where
p
c
is the probability in
S
of class label
c
. The entropy of
S
after splitting on attribute
A
is
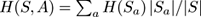 , where
S
a
is the subset of
S
where
A
has value
a
. The information gain of
A
is then
IG
(
S,A
) =
H
(
S
) −
H
(
S,A
). This measure was made popular after the C4.5 decision tree algorithm.
, where
S
a
is the subset of
S
where
A
has value
a
. The information gain of
A
is then
IG
(
S,A
) =
H
(
S
) −
H
(
S,A
). This measure was made popular after the C4.5 decision tree algorithm.
-
Gini impurity reduction, that is, the difference between the Gini index before and after splitting by the attribute. This measure was made popular after the CART decision tree algorithm. The Gini index of a random variable
C
is another nonlinear measure of the dispersion of
C
, defined as
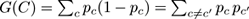 .
.
6.3.1 Estimating Split Criteria
The measures above need to be estimated from finite samples, but in a way that generalizes to future examples (that is, whether it is made now or in a month, year, or decade hence, it will still be the same decision, assuming stationarity). This calls for concentration inequalities in the spirit of those presented in section 4.2, which bound the probability that an estimate over a finite sample is far off its expectation.
Hoeffding’s inequality has often been used for estimating measures like information gain or the Gini index. Unfortunately, these measures cannot be expressed as a sum of independent random variables, and so Hoeffding’s bound is argued in recent work by Rutkowski et al. [ 218 ] to be the wrong tool.
A generalization of Hoeffding’s inequality called McDiarmid’s inequality can, however, be used for making split decisions using these measures as it works explicitly on functions of the data [
218
]. For information gain
IG
, the following can be shown for any two attributes
A
and
B
: if E
S
[
IG
(
S,A
) −
IG
(
S,B
)]
>
𝜖
, then with probability 1 −
δ
we have
IG
(
S,A
) −
IG
(
S,B
) > 0, where
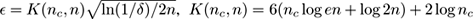 ,
n
is the size of
S
, and
n
c
is the number of classes. The formulation for the Gini index is simpler: it suffices to have
,
n
is the size of
S
, and
n
c
is the number of classes. The formulation for the Gini index is simpler: it suffices to have
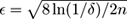 . Similar bounds are given in [
215
]. Misclassification error can also be used [
217
], eventually giving a bound very similar to Hoeffding’s bound.
. Similar bounds are given in [
215
]. Misclassification error can also be used [
217
], eventually giving a bound very similar to Hoeffding’s bound.
Note that our description of work on decision trees for streaming takes a historical perspective. The use of McDiarmid’s bound is cutting-edge for this particular method and represents a relatively new result. Hoeffding trees may, in the future, be proven incorrect in the sense of being based on assumptions that do not hold, however, they are still very effective in practice, and so worthy of study.
6.3.2 The Hoeffding Tree
In the data stream setting, where we cannot store all the data, the main problem of building a decision tree is the need to reuse instances to compute the best splitting attributes. Domingos and Hulten [ 88 ] proposed the Hoeffding Tree, a very fast decision tree algorithm for streaming data, where instead of reusing instances, we wait for new instances to arrive. The most interesting feature of the Hoeffding Tree is that it builds a tree that provably converges to the tree built by a batch learner with sufficiently large data; a more precise statement of this equivalence is provided later in this section.
The pseudocode of the Hoeffding Tree is shown in figure 6.3 . It is based on Hoeffding’s bound, discussed in section 4.2. On the basis of the bound, the proposal in [ 88 ] was to choose, as a confidence interval for the estimation of the entropy at a node, the value
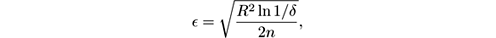
where R is the range of the random variable, δ is the desired probability of the estimate not being within 𝜖 of its expected value, and n is the number of examples collected at the node. In the case of information gain, the entropy is in the range [0,…,log n c ] for n c class values. Although the use of Hoeffding’s bound in this context is formally incorrect, as explained before, it is still used in most implementations; the reasonable results it achieves may be due to the fact that it gives, in most cases, an overestimation of the true probability of error.

Figure 6.3
The Hoeffding Tree algorithm.
The Hoeffding Tree algorithm maintains in each node the statistics needed for splitting attributes. For discrete attributes, this is the same information as needed for computing the Naive Bayes predictions: a 3-dimensional table that stores for each triple ( x i ,v j ,c ) a count n i,j,c of training instances with x i = v j , together with a 1-dimensional table for the counts of C = c . The memory needed depends on the number of leaves of the tree, not on the length of the data stream.
A theoretically appealing feature of the Hoeffding Tree not shared by other incremental decision tree learners is that it has sound guarantees of performance. It was shown in [ 88 ] that its output is asymptotically nearly identical to that of a nonincremental learner using infinitely many examples, in the following sense.
The intensional disagreement Δ i between two decision trees DT 1 and DT 2 is the probability that the path of an example through DT 1 will differ from its path through DT 2 , in length, or in the attributes tested, or in the class prediction at the leaf. The following result is rigorously proved in [ 88 ]: Let HT δ be the tree produced by the Hoeffding Tree algorithm with parameter δ from an infinite stream of examples, DT be the batch tree built from an infinite batch, and p be the smallest probability of a leaf in DT . Then we have E [Δ i ( HT δ ,DT )] ≤ δ/p .
Domingos and Hulten [ 88 ] improved the Hoeffding Tree algorithm to a more practical method called the very fast decision tree (VFDT), with the following characteristics:
- Ties: When two attributes have similar split gain G , the improved method splits if Hoeffding’s bound is lower than a certain threshold parameter τ .
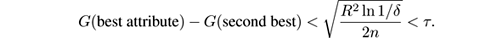
- To speed up the process, instead of computing the best attributes to split every time a new instance arrives, the VFDT computes them every time a number n min of instances has arrived.
-
To reduce the memory used in the mining, the VFDT deactivates the least promising nodes, those with the lowest product
p
l
×
e
l
, where
- p l is the probability to reach leaf l , and
- e l is the error in node l .
- The method can be started from any preexisting decision tree, for example, one built from an available batch of data. Hoeffding trees can grow slowly and performance can be poor initially, so this extension provides an immediate boost to the learning curve.
It is worth noting that there has been very little research on the last point in the VFDT method. Slow initial learning is an issue for these trees, and bootstrapping via an initial decision tree to create a better starting point makes sense.
One way to improve the classification performance of the Hoeffding Tree is to use Naive Bayes learners at the leaves instead of the majority class classifier. Gama and Medas [ 113 ] were the first to use Naive Bayes in Hoeffding Tree leaves, replacing the majority class classifier. However, Holmes et al. [ 135 ] identified situations where the Naive Bayes method outperforms the standard Hoeffding Tree initially but is eventually overtaken. To solve that, they proposed a hybrid adaptive method that generally outperforms the two original prediction methods for both simple and complex concepts: when performing a prediction on a test instance, the leaf will return the Naive Bayes prediction if it has been more accurate overall than the majority class prediction, otherwise it returns the majority class. The only overhead is keeping the two counts for the number of times each classifier has been correct.
6.3.3 CVFDT
Hulten et al. [ 138 ] presented the concept-adapting very fast decision tree (CVFDT) algorithm as an extension of VFDT to deal with concept drift, maintaining a model that is consistent with the instances stored in a sliding window. Unfortunately, such trees do not have theoretical guarantees like Hoeffding trees. Note that, theoretically, Hoeffding trees can to some extent adapt to concept drift, because leaves that would not grow any more under a stationary distribution may start to grow again if evidence gathers that further splitting would improve accuracy. However, this process is too slow in practice.
Figure 6.4 shows a sketch of the code for the CVFDT algorithm; a fuller description is provided in the reference above. It is similar to the code for the Hoeffding Tree but with the changes listed below. Note that here we use the terms “remove” and “forget” which look the same. They are different, however, as forgetting is a complex procedure that removes an instance from the tree. In contrast, adding and removing instances only applies to the sliding window.

Figure 6.4
The CVFDT algorithm.
- The main method maintains a sliding window with the latest instances, so it has to add, remove, and forget instances.
- The main method calls procedure CVFDTG ROW to process an example, but also method C HECK S PLIT V ALIDITY to check whether the chosen splits are still valid.
- CVFDTG ROW also updates counts of the nodes traversed in the sort.
- C HECK S PLIT V ALIDITY creates an alternate subtree if the attributes chosen to split are now different from the ones that were chosen when the split was done.
- Periodically, the algorithm checks whether the alternate branch is performing better than the original branch tree, and if so it replaces the original branch, and if not, it removes the alternate branch.
6.3.4 VFDTc and UFFT
VFDTc and UFFT are two methods that extend the Hoeffding Tree to handle numeric attributes and concept drift. VFDTc, developed by Gama et al. [ 111 ], does the following:
- It keeps Naive Bayes learners at the leaves to make predictions.
- It handles numeric attributes using binary trees, as explained in section 6.4.2.
- To handle concept drift, it uses the statistical DDM method explained in section 5.3.4.
The ultra fast forest of trees (UFFT), developed by Gama and Medas [ 113 ], generates a forest of binary trees, one for each possible pair of classes. The trees contain a Naive Bayes classifier at each node, like VFDTc. The main difference from VFDTc is in the handling of numeric attributes.
UFFT uses analytical techniques to choose the splitting criteria, and information gain to estimate the merit of each possible splitting test. For multiclass problems, the algorithm builds a binary tree for each possible pair of classes, leading to a forest of trees, that comprises k ( k − 1)/2 classifiers for a k -class problem. The analytical method uses a modified form of quadratic discriminant analysis to include different variances on the two classes.
6.3.5 Hoeffding Adaptive Tree
The Hoeffding Adaptive Tree [ 33 ] is an adaptive extension to the Hoeffding Tree that uses A DWIN as a change detector and error estimator. It has theoretical guarantees of performance and requires no parameters related to change control. In contrast, CVFDT has no theoretical guarantees, and requires several parameters with default values that can be changed by the user, but which are fixed for a given execution. It requires:
- W : The example window size.
- T 0 : Every T 0 examples, CVFDT traverses the entire decision tree, and checks at each node whether the splitting attribute is still the best. If there is a better splitting attribute, it starts growing an alternate tree rooted at this node, and it splits on the current best attribute according to the statistics at the node.
- T 1 : After an alternate tree is created, the following T 1 examples are used to build the alternate tree.
- T 2 : After the arrival of T 1 examples, the following T 2 examples are used to test the accuracy of the alternate tree. If the alternate tree is more accurate than the current one, CVFDT replaces it with this alternate tree (we say that the alternate tree is promoted).
The default values are W = 50,000, T 0 = 10,000, T 1 = 9,000, and T 2 = 1,000. We can interpret these figures as the assumptions that often the last 50,000 examples are likely to be relevant, that change is not likely to occur faster than every 10,000 examples, and that 1,000 examples will be sufficient to tell the best among current and candidate trees. These assumptions may or may not be correct for a given data source. Moreover, the stream may change differently at different times, so no single set of values may be best for all the stream.
The main differences of the Hoeffding Adaptive Tree with respect to CVFDT are:
- The alternate trees are created as soon as change is detected, without having to wait for a fixed number of examples to arrive after the change. Furthermore, the more abrupt the change, the faster a new alternate tree will be created.
- The Hoeffding Adaptive Tree replaces an old tree with the alternate tree as soon as there is evidence that it is more accurate, rather than waiting for another fixed number of examples.
These two effects can be summarized by saying that the Hoeffding Adaptive Tree adapts to the scale of time change in the data, rather than relying on the a priori guesses made by the user.
6.4 Handling Numeric Attributes
Handling numeric attributes in a data stream classifier is much more difficult than in a nonstreaming setting. In this section we will review the most popular methods used for discretization in decision trees and Naive Bayes algorithms in evolving data streams. We need to examine how to manage the statistics of numeric attributes and how to determine the best splitting points in decision trees.
We start by mentioning the methods in the nonstreaming scenario. There, the main discretization strategies are:
- Equal width: The range of the numeric attribute is divided into a fixed quantity of bins of the same size. The maximum and minimum values are needed to compute the upper and lower values in the bins. This is the simplest method as it does not need to sort the data, but it is vulnerable to the existence of outliers and to skewed distributions.
- Equal frequency: This strategy also uses a fixed number of bins, but each bin contains the same number of elements. For n values and k bins, the bin weight will be n/k , up to rounding. It is well suited for outliers and skewed distributions, but it needs more processing time, as it needs to sort the values.
- Fayyad and Irani’s method [ 98 ]: This is based on computing the best cut-points using information gain as it is used in decision trees. First, it sorts the data, and then each point between adjacent pairs of values is selected as a split candidate. Using information gain, the best cut-point is selected, and then the procedure continues recursively in each of the parts. A stopping criterion is needed to stop the recursive process. The criterion is based on stopping when intervals become pure, with values of one class only, or when the minimum description length principle estimates that dividing the numeric range will not bring any further benefit.
6.4.1 VFML
The very fast machine learning (VFML) package of Hulten and Domingos [ 137 ] contains a method for handling numeric attributes in VFDT and CVFDT. Numeric attribute values are summarized by a set of ordered bins. The range of values covered by each bin is fixed at creation time and does not change as more examples are seen. A hidden parameter serves as a limit on the total number of bins allowed—in the VFML implementation this is hard-coded to allow a maximum of 1,000 bins. Initially, for every new unique numeric value seen, a new bin is created. Once the fixed number of bins have been allocated, each subsequent value in the stream updates the counter of the nearest bin.
Essentially, the algorithm summarizes the numeric distribution with a histogram, made up of a maximum of 1,000 bins. The boundaries of the bins are determined by the first 1,000 unique values seen in the stream, and after that the counts of the static bins are incrementally updated.
There are two potential issues with this approach. Clearly, the method is sensitive to data order. If the first 1,000 examples seen in a stream happen to be skewed to one side of the total range of values, then the final summary cannot accurately represent the full range of values.
The other issue is estimating the optimal number of bins. Too few bins will mean the summary is small but inaccurate, whereas too many bins will increase accuracy at the cost of space. In the experimental comparison the maximum number of bins is varied to test this effect.
6.4.2 Exhaustive Binary Tree
Gama et al. [ 111 ] present this method in their VFDTc system. It aims at achieving perfect accuracy at the expense of storage space. The decisions made are the same that a batch method would make, because essentially it is a batch method—no information is discarded other than the order of values.
It works by incrementally constructing a binary tree as values are observed. The path a value follows down the tree depends on whether it is less than, equal to, or greater than the value at a particular node in the tree. The values are implicitly sorted as the tree is constructed, and the number of nodes at each time is the number of distinct values seen. Space saving occurs if the number of distinct values is small.
On the other hand, the structure saves search time versus storing the values in an array as long as the tree is reasonably balanced. In particular, if values arrive in order, then the tree degenerates to a list and no search time is saved.
6.4.3 Greenwald and Khanna’s Quantile Summaries
The field of database research is also concerned with the problem of summarizing the numeric distribution of a large dataset in a single pass and limited space. The ability to do so can help to optimize queries over massive databases.
Greenwald and Khanna [ 129 ] proposed a quantile summary method with even stronger accuracy guarantees than previous approaches. The method works by maintaining an ordered set of tuples, each of which records a value from the input stream, along with implicit bounds for the range of each value’s true rank. Precisely, a tuple t i = ( v i ,g i ,Δ i ) consists of three values:
- a value v i of one of the elements seen so far in the stream,
- a value g i that equals r min ( v i ) − r min ( v i −1 ), where r min ( v ) is the lower bound of the rank of v among all the values seen so far, and
- a value Δ i that equals r max ( v i ) − r min ( v i ), where r max ( v ) is the upper bound of the rank of v among all the values seen so far.
Note that
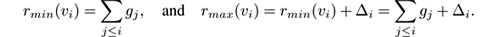
The quantile summary is 𝜖 -approximate in the following sense: after seeing N elements of a sequence, any quantile estimate returned will not differ from the exact value by more than 𝜖 N . An operation for compressing the quantile summary is defined that guarantees max( g i + Δ i ) ≤ 2 𝜖 N , so that the error of the summary is kept within 2 𝜖 .
The worst-case space requirement is shown to be
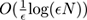 , with empirical evidence showing it to be even better than this in practice.
, with empirical evidence showing it to be even better than this in practice.
6.4.4 Gaussian Approximation
This method, presented in [ 199 ], approximates a numeric distribution in small constant space, using a Gaussian or normal distribution. Such a distribution can be incrementally maintained by storing only three numbers, in a way that is insensitive to data order. A similar method to this one was described by Gama and Medas in their UFFT system [ 113 ].
For each numeric attribute, the method maintains a separate Gaussian distribution per class label. The possible values are reduced to a set of points spread equally across the range, between the minimum and maximum values observed. The number of evaluation points is determined by a parameter, so the search for split points is parametric , even though the underlying Gaussian approximations are not. For each candidate point, the weight of values to either side of the split can be approximated for each class, using their respective Gaussian curves, and the information gain is computed from these weights.
The process is illustrated in figure 6.5 . At the top of the figure are two Gaussian curves, each approximating the distribution of values for a numeric attribute and labeled with a particular class. Each curve can be described using three values: the mean, the variance, and the total weight of examples. For instance, in figure 6.5 , the class shown to the left has a lower mean, higher variance, and higher example weight (larger area under the curve) than the other class. Below the curves, the range of values has been divided into ten split points, labeled A to J. The vertical bar at the bottom displays the relative amount of information gain calculated for each split. The split point that would be chosen as the best is point E, which the evaluation shows has the highest information gain.
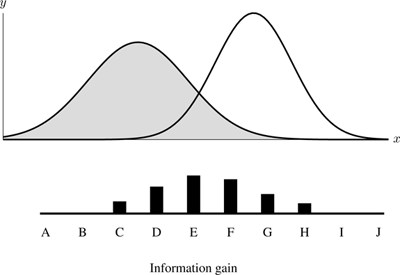
Figure 6.5
Gaussian approximation of two classes. Figure based on [
199
].
A refinement of this method involves also tracking the minimum and maximum values of each class. This requires storing an extra two counts per class, but they are simple and take little time to maintain. When evaluating split points, the method exploits per-class minimum and maximum information to determine when class values lie completely to one side of a split, eliminating the small uncertainty otherwise present in the tails of the Gaussian curves. From the per-class minimum and maximum, the minimum and maximum of the entire range of values can be established, which helps to determine the position of split points to evaluate.
Approximation by a sum of Gaussians will almost certainly not capture the full detail of an intricate numeric distribution, but the approach is efficient in both computation and memory. Whereas the binary tree method uses extreme memory costs to be as accurate as possible, this method employs the opposite approach—using gross approximation to use as little memory as possible. And in fact, the simplified view of numeric distributions is not necessarily harmful to the accuracy of the trees it produces. There will be further opportunities to refine split decisions on a particular attribute by splitting again further down the tree. Also, the approximation by a few simple parameters can be more robust and resistant to noise and outliers than more complicated methods, which concentrate on finer details.
6.5 Perceptron
The Perceptron, proposed by Rosenblatt in 1957, is a linear classifier and one of the first methods for online learning. Because of its low computational cost, it was shown in [ 37 ] to be a useful complement to the Majority Class and Naive Bayes classifiers at the leaves of decision trees.
The algorithm is given a stream of pairs
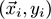 , where
, where
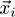 is the
i
th example and
y
i
is its class. The perceptron keeps at all times a vector of weights
is the
i
th example and
y
i
is its class. The perceptron keeps at all times a vector of weights
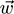 that defines the function
that defines the function
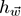 used to label examples; in particular, for every example
used to label examples; in particular, for every example
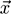 we have
we have
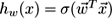 , where
, where
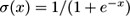 is a soft-threshold function whose range is [0,1]. The prediction given to the outside is more likely produced by applying the sign function (i.e., a 0 or 1 value), but
using
σ
is more convenient for the derivation of the update rule. A nonzero decision threshold can be simulated by adding an additional feature in
x
that is always 1.
is a soft-threshold function whose range is [0,1]. The prediction given to the outside is more likely produced by applying the sign function (i.e., a 0 or 1 value), but
using
σ
is more convenient for the derivation of the update rule. A nonzero decision threshold can be simulated by adding an additional feature in
x
that is always 1.
The derivation of the update rule can be found in many texts on ML, and is omitted here. In essence, its goal is to update the weights
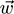 to minimize the number of misclassified examples, and this is achieved by moving each component of
to minimize the number of misclassified examples, and this is achieved by moving each component of
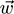 in the direction of the gradient that decreases the error. More precisely, the rule is:
in the direction of the gradient that decreases the error. More precisely, the rule is:
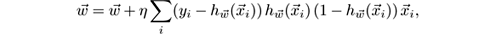
where η is a parameter called the learning rate .
This method is the simplest example of so-called stochastic gradient descent for incremental optimization of a loss function on a set or stream of examples.
6.6 Lazy Learning
Perhaps the most obvious batch method to try in the streaming context is the k -nearest neighbor method, k -NN [ 209 ]. The change to streaming is readily achieved by using a sliding window as the search space for determining the k -nearest neighbors to a new unclassified instance, and predicting the majority among their k labels. Votes can optionally be weighted by the inverse of the distance to the point to predict, or some other scheme. The method using a sliding window with the 1,000 most recent instances was found to be remarkably effective in [ 209 ].
As the window slides, the method naturally responds to concept drift. Concept drift can be either abrupt or gradual, and responding to these differently makes sense for lazy learners [ 28 ].
If implemented naively, the method is generally inefficient at prediction time because of the search for neighbors, but it is possible to index the instances in the sliding window to improve prediction efficiency [ 257 ].
More recently, Losing et al. [ 162 ] proposed the use of two memories for coping with different concept drift types and drift speeds. A short-term memory, containing data from the most current window, is used to model the current concept, and a long-term memory is used to maintain knowledge of past concepts. By carefully managing these two memories, very competitive results can be achieved in benchmark tests. The authors point out that the method is useful in practice because it does not require any meta-parameters to be tuned.
Some variant of k -NN, even just the simplest one, should always be used when evaluating new classification methods.
6.7 Multi-label Classification
In many real-world applications, particularly those involving text, we are faced with multiclass problems: classifying instances into multiple class labels rather than only one. An example in text categorization is applying tags to documents. Imagine that we are tagging news articles, and we have to tag an article about a rugby game between France and New Zealand. That document can be classified as both France and New Zealand , as well as rubgy and possibly sports . There are many other applications: scene and video classification, medical diagnosis, and applications in microbiology.
The main challenge in multi-label classification is detecting and modeling dependencies between labels, without becoming too complex computationally. A simple baseline method is binary relevance (BR). BR transforms a multi-label problem into multiple binary problems, such that binary models can be employed to learn and predict the relevance of each label. An advantage of the method is that it is quite resistant to labelset overfitting, since it learns on a per-label basis. It has often been overlooked in the literature because it fails to take into account label correlations directly during the classification process [ 123 , 210 , 235 ], although there are several methods that overcome this limitation [ 68 , 123 , 211 ]. For example, in [ 211 ] Read et al. introduced ensembles of BR classifiers, and also the concept of classifier chains , both of which improve considerably on BR in terms of predictive performance.
A problem for BR methods in data streams is that class-label imbalance may become exacerbated by large numbers of training examples. Countermeasures to this are possible, for example by using per-label thresholding methods or classifier weightings as in [ 203 ].
BR can be applied directly to data streams by using streaming binary base models. Additional advantages in the streaming setting are BR’s low time complexity and the fact that it can be easily parallelized.
An alternative paradigm to BR is the label combination or label powerset method (LC). LC transforms a multi-label problem into a single-label (multiclass) problem by treating all label combinations as atomic labels, that is, each labelset in the training set becomes a single class-label within a single-label problem. Thus, the set of single class-labels represents all distinct label subsets in the original multi-label representation, so label correlations are taken into account. Disadvantages of LC include its worst-case computational cost (as there are potentially up to 2 L labelsets on L labels) and a strong tendency to overfit the training data, although this problem has been largely overcome by newer methods [ 210 , 235 ]; ideas include, for example, taking random label subsets from the labelset to train an ensemble of classifiers, as well as various pruning strategies.
A particular challenge for LC methods in a data stream context is that the label space expands over time due to the emergence of new label combinations. It is possible to adapt probabilistic models to account for the emergence of new labelset combinations over time; however, probabilistic models are not necessarily the best-performing ones. A general “buffering” strategy may be useful [ 208 ], where label combinations are learned from an initial number of examples and these are considered sufficient to represent the distribution. During the buffering phase, another model can be employed to adhere to the “ready to predict at any point” requirement.
Another multi-label approach is pairwise classification (PW), where binary models are used for every possible pair of labels [ 109 ]. PW performs well in some contexts, but the complexity in terms of models—namely, L × ( L − 1)/2 for L labels—demands new ideas to make it applicable to large problems.
Note that these are all problem transformation methods, wherein a multi-label problem is transformed into one or more single-label problems, after which any off-the-shelf multi-class classifier (or binary, in the case of BR and PW) can be used. These methods are interesting generally due to their flexibility and general applicability.
The iSOUP-Tree (incremental structured output prediction) method [ 188 ] is a multi-label classifier that performs multi-label classification via multitarget regression. There exist two variants of the iSOUP-Tree method (building regression and model trees), as well as ensembles of iSOUP-Trees.
6.7.1 Multi-label Hoeffding Trees
A Multi-label Hoeffding tree was presented in [ 208 ], based on adaptation of the information gain criterion to multi-label problems.
Recall that Hoeffding trees use the information gain criterion to decide the best attribute at each expanding node, and that the information gain of an attribute is the difference between the entropy of the dataset before and after the split. As entropy measures the amount of uncertainty in the dataset, in the case of multi-label examples, we need to add to the entropy the information needed to describe all the classes that an example does not belong to.
Clare and King [ 72 ] showed that this can be accomplished by adding to the regular entropy a term that adds, for each label, a quantity related to the class entropy in the examples having that label. From there, they proposed a multi-label version of C4.5. The Multi-label Hoeffding Tree [ 208 ] uses this strategy to construct a decision tree. A Majority Labelset Classifier (the multi-label version of Majority Class) is used as the default classifier on the leaves of a Multi-label Hoeffding tree. However, any multi-label classifier at the leaves can be used.
6.8 Active Learning
Classifier methods need labeled training data to build models. Often unlabeled data is abundant but labeling is expensive. Labels can be costly to obtain due to the required human input (labor cost). Consider, for example, textual news arriving as a stream. The goal is to predict whether a news item will be interesting to a given user at a given time, and the interests of the user may change. To obtain training data the historical news needs to be read and labeled as interesting or not interesting. Currently this requires human labor. Labeling can also be costly due to a required expensive, intrusive, or destructive laboratory test. Consider a production process in a chemical plant where the goal is to predict the quality of production output. The relationship between input and output quality might change over time due to constant manual tuning, complementary ingredients, or replacement of physical sensors. In order to know the quality of the output (the true label) a laboratory test needs to be performed, which is costly. Under such conditions it may be unreasonable to require true labels for all incoming instances.
Active learning algorithms ask for labels selectively instead of expecting to receive all the instance labels. This has been extensively studied in pool-based [ 157 ] and online settings [ 77 ]. In pool-based settings, the decision concerning which instances to label is made from all historical data.
In [ 261 ], a framework setting for active learning in evolving data streams was presented. It works as follows: Data arrives in a stream, and predictions need to be made in real time. Concept drift is expected, so learning needs to be adaptive. The true label can be requested immediately or never, as the instances are regularly discarded from memory. The goal is to maximize prediction accuracy over time, while keeping the labeling costs fixed within an allocated budget. After scanning an instance and outputting the prediction for it, we need a strategy to decide whether or not to query for the true label, so that our model could train itself with this new instance. Regular retraining is needed due to changes in data distribution. Active learning strategies in data streams, in addition to learning an accurate classifier in stationary situations, must be able to
- balance the labeling budget over time,
- notice changes happening anywhere in the instance space, and
- preserve the distribution of the incoming data for detecting changes.
More formally, the setting is as follows: The algorithm receives a stream of unlabeled instances x t and a budget B , expressing the fraction of past instances that it is allowed to ask for labeling. If it requests the label for x t , the algorithm receives the true label of x t , denoted y t . The cost of obtaining a label is assumed to be the same for all instances. B = 1 means that all arriving instances can be labeled, whereas B = 0.2 means that, at any moment, the algorithm may have requested the labels of at most 20% of the instances seen so far.
Figure 6.6 shows the framework that combines active learning strategies with adaptive learning. This framework uses the change detection technique of [ 114 ]: when the accuracy of the classifier begins to decrease, a new classifier is built and trained with new incoming instances. When a change is detected, the old classifier is replaced by the new one.

Figure 6.6
Active learning framework.
Next we describe four of the strategies proposed for budget allocation.
6.8.1 Random Strategy
The first (baseline) strategy is naive in the sense that it labels the incoming instances at random instead of actively deciding which label would be most relevant. For every incoming instance the true label is requested with probability B , where B is the budget.
6.8.2 Fixed Uncertainty Strategy
Uncertainty sampling is perhaps the simplest and the most common active learning strategy [ 224 ]. The idea is to label the instances for which the current classifier is the least confident. In an online setting, this corresponds to labeling the instances for which the certainty is below some fixed threshold. A simple way to measure uncertainty is to use the posterior probability estimates, output by a classifier.
6.8.3 Variable Uncertainty Strategy
One of the challenges with the fixed uncertainty strategy in a streaming data setting is how to distribute the labeling effort over time. Using a fixed threshold, after some time a classifier will either exhaust its budget or reach the threshold certainty. In both cases it will stop learning and thus fail to adapt to changes.
Instead of labeling the instances that are less certain than the threshold, we want to label the least certain instances within a time interval. Thus we can introduce a variable threshold, which adjusts itself depending on the incoming data to align with the budget. If a classifier becomes more certain (stable situations), the threshold expands to be able to capture the most uncertain instances. If a change happens and suddenly a lot of labeling requests appear, then the threshold is contracted to query only the most uncertain instances.
It may seem counterintuitive to ask for more labels in quiet periods and fewer labels at change points. But, in fact, this ensures that the algorithm asks for the same fraction of labels in all situations. Since it does not know when or how often changes will be happening, this helps in spending the budget uniformly over time.
The variable uncertainty strategy is described in figure 6.7 . More detail and a comparison with the other strategies can be found in [ 261 ].

Figure 6.7
Variable uncertainty strategy, with a dynamic threshold.
6.8.4 Uncertainty Strategy with Randomization
The uncertainty strategy always labels the instances that are closest to the decision boundary of the classifier. In data streams, changes may happen anywhere in the instance space. When concept drift happens in labels, the classifier will not notice it without the true labels. In order to not miss concept drift we should, from time to time, label some instances about which the classifier is very certain. For that purpose, for every instance, the strategy randomizes the labeling threshold by multiplying by a normally distributed random variable that follows N (1 , δ ). This way, it labels the instances that are close to the decision boundary more often, but occasionally also labels some distant instances.
This strategy trades off labeling some very uncertain instances for labeling very certain instances, in order to not miss changes. Thus, in stationary situations this strategy is expected to perform worse than the uncertainty strategy, but in changing situations it is expected to adapt faster.
Table 6.3 summarizes the four strategies with respect to several requirements. The random strategy satisfies all three requirements. Randomized uncertainty satisfies budget and coverage, but it produces biased labeled data. Variable uncertainty satisfies only the budget requirement, and fixed uncertainty satisfies none.
Table 6.3
Summary of budget allocation strategies.
|
Controlling budget |
Instance space coverage |
Labeled data distribution |
|
|
Random |
present |
full |
IID |
|
Fixed uncertainty |
no |
fragment |
biased |
|
Variable uncertainty |
handled |
fragment |
biased |
|
Randomized uncertainty |
handled |
full |
biased |
6.9 Concept Evolution
Concept evolution occurs when new classes appear in evolving data streams. For example, in mining text data from Twitter, new topics can appear in tweets; or in intrusion detection in network data streams, new types of attacks can appear, representing new classes.
Masud et al. [ 170 ] were the first to deal with this setting. Their approach consists of training an ensemble of k -NN-based classifiers that contain pseudo-points obtained using a semisupervised k -means clustering. Each member of the ensemble is trained on a different labeled chunk of data. New instances are classified using the majority vote among the classifiers in the ensemble.
Each pseudopoint represents a hypersphere in the feature space with a corresponding centroid and radius. The decision boundary of a model is the union of the feature spaces; and the decision boundary of the ensemble is the union of the decision boundaries of all the models in the ensemble.
Each new instance is first examined by the ensemble of models to see if it is outside the decision boundary of the ensemble. If it is inside the decision boundary, then it is classified normally using the majority vote of the models of the ensemble. Otherwise, it is declared as an F-outlier, or filtered outlier. These F-outliers are potential novel class instances, and they are temporarily stored in a buffer to observe whether they are close to each other. This is done by using a q -neighborhood silhouette coefficient (q-NSC), a unified measure of cohesion and separation that yields a value between −1 and +1. A positive value indicates that the point is closer to the F-outlier instances (more cohesion) and farther away from existing class instances (more separation), and vice versa. A new class is declared if there are a sufficient number of F-outliers having positive q-NSC for all classifiers in the ensemble.
The SAND (semisupervised adaptive novel detection) method [ 133 ] determines the chunk size dynamically based on changes in the classifier confidence. SAND is thus more efficient and avoids unnecessary training during periods with no changes.
Finally, in [ 10 ], a “class-based” ensemble technique is presented that replaces the traditional “chunk-based” approach in order to detect recurring classes. The authors claim that the class-based ensemble methods are superior to the chunk-based techniques.
6.10 Lab Session with MOA
In this session lab you will use MOA through the graphical interface to learn several classifier models and evaluate them in different ways. The initial MOA GUI screen is shown in figure 6.8 .
Figure 6.8
MOA graphical user interface.
Exercise 6.1
Click
Configure
to set up a task. Change the task type in the dropdown menu at the top to
LearnModel
. As you can see, the default learner is
NaiveBayes
. You could change it by clicking the
Edit
button and then selecting from the dropdown menu at the top. However, leave it as
NaiveBayes
for now. The default data stream is
RandomTreeGenerator
. Use the corresponding
Edit
button to change it to
WaveformGenerator
, which generates instances from a combination of waveforms. Change the number of instances to generate from 10,000,000 to 1,000,000. Finally, specify a
taskResultFile
, say
modelNB.moa
, where MOA will output the model.
Now click OK, and then Run to launch this task. Textual output appears in the center panel: in this case, every 10,000 steps. Various evaluation measures appear in the lower panel, and are continuously updated until the task completes. MOA can run several tasks concurrently, as you will see if you click Run twice in quick succession. Clicking on a job in the top panel displays its information in the lower two panels.
The task you have just run is
LearnModel -l bayes.NaiveBayes
-s generators.WaveformGenerator
-m 1000000 -O modelNB.moa
—
you can see this in the line beside the
Configure
button—and it has stored the Naive Bayes model in the file
modelNB.moa
. (However, parameters that have their default value are not shown in the configuration text.)
Click
Configure
and change the learner to a Hoeffding Tree with output file
modelHT.moa
:
LearnModel -l trees.HoeffdingTree
-s generators.WaveformGenerator
-m 1000000 -O modelHT.moa
and run it. Now we have two models stored on disk,
modelNB.moa
and
modelHT.moa
.
We will evaluate the Naive Bayes model using
1,000,000
new instances generated by the
WaveformGenerator
, which is accomplished by the task
EvaluateModel -m file:modelNB.moa
-s (generators.WaveformGenerator -i 2) -i 1000000
The
-i 2
sets a different random seed for the waveform generator. You can set up most of these in the
Configure
panel: at the top, set the task to
EvaluateModel
, and configure the stream (which has now changed to
RandomTreeGenerator
) to
WaveformGenerator
with
instanceRandomSeed
equal to 2. Frustratingly, though, you cannot specify that the model should be read from a file.
It is useful to learn how to get around such problems. Click
OK
to return to the main MOA interface, select
Copy configuration to clipboard
from the right-click menu, then select
Enter configuration
and paste the clipboard into the new configuration, where you can edit it, and type
-m file:modelNB.moa
into the command line. This gives the
EvaluateModel
task the parameters
needed to load the Naive Bayes model produced in the previous step, generate a new waveform stream with a random seed of 2, and test on
1,000,000
examples.
a. What is the percentage of correct classifications?
b. Edit the command line to evaluate the Hoeffding Tree model. What is the percentage of correct classifications?
c. Which model performs best according to the Kappa statistic?
Exercise 6.2
In MOA, you can nest commands. For example, the
LearnModel
and
EvaluateModel
steps can be rolled into one, avoiding the need to create an external file. You cannot do this within the interactive
Configure interface; instead you have to edit the Configure command text.
OzaBag
is an incremental bagging technique that we will see in the next chapter. Evaluate it as follows:
EvaluateModel -m (LearnModel -l meta.OzaBag
-s generators.WaveformGenerator -m 1000000)
-s (generators.WaveformGenerator -i 2) -i 1000000
Do this by copying this command and pasting it as the Configure text using right-click, Enter configuration.
What is the accuracy of
OzaBag
?
Exercise 6.3
The task
EvaluatePeriodicHeldOutTest
trains a model while taking performance snapshots at periodic intervals on a holdout test set.
a. The following command trains the
HoeffdingTree
classifier on 10,000,000 samples from the
WaveformGenerator
data, after holding out the first 100,000 samples as a test set; after every 1,000,000 examples it performs a test on this set:
EvaluatePeriodicHeldOutTest -l trees.HoeffdingTree
-s generators.WaveformGenerator
-n 100000 -i 10000000 -f 1000000
You can copy this configuration and paste it in (cheating!), or set it up in the interactive Configure interface (test size 100,000, train size 10,000,000, sample frequency 1,000,000). It outputs a CSV file with 10 rows in the center panel and final statistics in the lower panel. What is the final accuracy?
b. What is the final Kappa statistic?
Exercise 6.4
Prequential evaluation evaluates first on any instance, then uses it to train. Here is an
EvaluatePrequential
task that trains a
HoeffdingTree
classifier on 1,000,000 examples of the
WaveformGenerator
data, testing every 10,000 examples, to create a 100-line CSV file:
EvaluatePrequential -l trees.HoeffdingTree
-s generators.WaveformGenerator
-i 1000000 -f 10000
Set it up in the interactive Configure interface and run it. At the bottom, the GUI shows a graphical display of the results—a learning curve. You can compare the results of two different tasks: click around the tasks and you will find that the current one is displayed in red and the previously selected one in blue.
a. Compare the prequential evaluation of
NaiveBayes
with
HoeffdingTree
. Does the Hoeffding Tree always outperform Naive Bayes in the learning curve display?
b. What is the final Kappa statistic for the Hoeffding Tree?
c. What is the final Kappa statistic for Naive Bayes?
Exercise 6.5
By default, prequential evaluation displays performance computed over a window of 1000 instances, which creates a jumpy, jagged learning curve. Look at the evaluator in the
Configure panel: you can see that the
WindowClassificationPerformanceEvaluator
is used, with a window size of
1000.
Instead, select the
BasicClassificationPerformanceEvaluator
, which computes evaluation measures from the beginning of the stream using every example:
EvaluatePrequential -l trees.HoeffdingTree
-s generators.WaveformGenerator
-e BasicClassificationPerformanceEvaluator
-i 1000000 -f 10000
As you can see, this ensures a smooth plot over time, because each individual example becomes less and less significant to the overall average.
a. Compare again the prequential evaluations of the Hoeffding Tree and Naive Bayes using the
BasicClassificationPerformanceEvaluator
. Does the Hoeffding tree always outperform Naive Bayes in the learning curve display?
b. What is the final Kappa statistic for the Hoeffding Tree?
c. What is the final Kappa statistic for Naive Bayes?