8.1 Introduction

Given a numeric attribute to be predicted, called the outcome , a regression algorithm builds a model that predicts for every unlabeled instance x a numeric prediction y for the outcome of x .

Examples of regression problems are predictions of quantities that cannot be reduced to a discrete label, such as prices in stock markets, product sales, time delays, or the number of visits to a website. It is possible to reduce regression to classification problems by discretizing the values of the outcome into intervals, or the other way around, to use regression algorithms to do classification, transforming the discrete class into a numerical variable. Of course, these transformations need not give optimal results.

The simplest regression algorithm is to return the mean value of the attribute that we want to predict. This is equivalent to the majority class method in classification, a learner that does not use the information in the rest of the attributes. A far more useful method in nonstreaming regression is linear regression .

Linear regression builds a linear model f , of the form

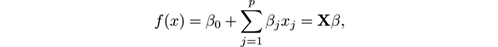
that minimizes the residual sum of squares:

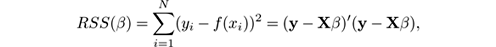
where the input is the set of N pairs ( x _i , y _i ). However, the exact solution is

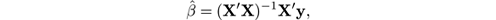
which is hard to compute incrementally, let alone in the streaming setting. Approximate solutions can be given using random projection sketches (see [ 73 , 248 ] for example), but their use in practical data mining is still preliminary. So we look for other strategies that are more clearly incremental and adaptive.

8.2 Evaluation

To evaluate regression methods, we can use the same methodologies as in classification, such as holdout, prequential, and Interleaved test-then-train, but the misclassification rate measure is not applicable. The following measures are usually considered in regression:

• Mean square error (MSE): This is the most common measure, and gives the error using the mean of the squares of the differences between the actual values and the predictions:

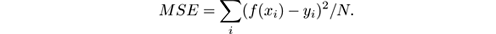
• Root mean square error: The square root of the mean square error:

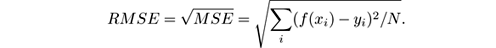
• Relative square error: The ratio between the MSE of the regression method, and the MSE of the simplest regression method available, the mean regression algorithm:

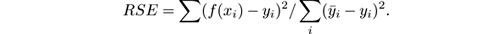
• Root relative square error: The square root of the relative square error:

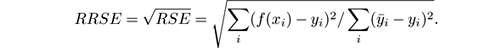
• Mean absolute error: This measure is similar to the MSE, but considers absolute values of the difference:

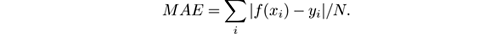
• Relative absolute error: Similar to the relative square error, but considers absolute values of the difference:

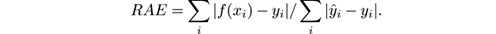
It is easy to see that all these measures can be computed incrementally by maintaining a constant number of values in memory.

8.3 Perceptron Learning

The Perceptron [ 37 ] was presented in section 6.5 as an online classification method. However, it is just as naturally viewed as a regression method.

Given a data stream of pairs 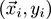, where 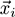is an example and y _i is its numeric outcome value, the goal of the perceptron is to minimize MSE on the examples. To do this, the strategy is again to move each weight in the weight vector 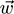in the direction of the descending error gradient.

The update rule becomes in this case:

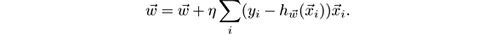
As in classification, weights can be updated at every single example, as in the weight above, or taken in mini-batches for a single update step per mini-batch. This allows us to fine-tune the trade-off between update time and adaptiveness.

8.4 Lazy Learning

Lazy learning is one of the simplest and most natural models for classification and regression—in particular the k -Nearest Neighbor algorithm. Given a distance function d among instances, the k -NN method in regression finds the k instances closest to the instance to predict, and averages their outcomes. As in classification, the average may be weighted according to the distance to each neighbor.

The performance of the method strongly depends on the distance function used. For dense instances with numeric attributes, the Euclidean distance could be appropriate. For textual data, the cosine similarity measure or the Jaccard coefficient could be more appropriate.

IBLStreams, due to Shaker and Hüllermeier [ 225 ], is an implementation of lazy learning for regression on streams. Besides the basic ideas from streaming k -NN, it includes heuristics for removing outlier points from the database, removing instances that are too close to some already in the database (hence, not that useful), and for adaptively choosing the size of the database and of the parameter k .

8.5 Decision Tree Learning

Fast Incremental Model Tree with Drift Detection (FIMT-DD) is a decision tree for streaming regression due to Ikonomovska et al. [ 139 ]. It is an extension of the Hoeffding Tree method that differs in the following areas:

• Splitting criterion: Variance reduction is used instead of information gain, that is, the attribute chosen is the one such that the variance 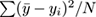is maximally reduced if splitting by this attribute.
• Numeric attributes: They are handled using an extension of the exhaustive binary tree method seen in section 6.4.2. At each node of the tree, the method stores a key value and keeps the following information for each of the two ranges ≤ key , or > key :
  • the sum of the values of the numeric outcome,
  • the sum of the square of the values of the outcome, and
  • a count of the number of instances.
• Pruning: Some pruning rules are used to avoid storing every single value of the outcome.
• Linear model at the leaves: Perceptrons are used at the leaves, to adapt to drift.
• Concept drift handling: The Page-Hinkley test is used at the inner nodes of the decision tree to detect changes in the error rate.
• Tree updates: When a subtree is underperforming, an alternate tree is grown with new incoming instances; it replaces the original tree when (and if) it performs better.

FIMT-DD overall behaves similarly to Hoeffding Trees for classification, and is one of the state-of-the-art methods for regression. An option tree for regression was presented later in [ 140 ].

8.6 Decision Rules

Decision rules are a formalism that combines high expressive power with high interpretability. Learning sets of decision rules has consequently received intense attention in the batch case. In the streaming case, the AMRules algorithm developed by Almeida, Ferreira, Gama, Duarte, and Bifet [ 12 , 13 , 90–92 ] is the first and still most popular rule-learning system.

AMRules stands for adaptive model rules, and is specifically designed so that rules can be added and removed from the ruleset as the stream evolves. A rule in AMRules is of the form A → M where:

• The antecedent A is a conjunction of literals and M is a model that emits a prediction.
• A literal is either a condition of the form A = a , where A is a discrete attribute and a one of its values, or of the form A ≤ v or A ≥ v , where A is continuous and v a real value. We say that a rule covers an example x if x satisfies all the conditions in the rule’s antecedent.
• Model M is a regression model. AMRules supports three types of regressors: (1) the mean of the target attribute computed from the examples covered by the rule; (2) a linear combination of the attributes; and (3) an adaptive strategy that chooses between (1) and (2), picking the one with lower MSE on recent examples.

AMRules maintains a set of rules that are neither exclusive nor complete, in the sense that they need not cover all examples and that an example may be covered by several rules. This differentiates it from decision trees, which can naturally be viewed as a set of exclusive and complete rules. A set of rules can be viewed as ordered or unordered; AMRules supports both views. If viewed as ordered, the prediction of an example is that of the first rule that covers it. If the rules are viewed as unordered, all rules that cover an example are evaluated and their predictions are averaged. In addition, AMRules maintains a distinguished default rule that has no antecedents and that is applied whenever no rule covers an example.

At the core of the algorithm are the methods for creating new rules, expanding existing rules, and deleting underperforming rules.

Rule expansion. In a way similar to the Hoeffding Tree for trees, for each rule and for each attribute, the algorithm monitors the standard deviation reduction (SDR) that would be introduced if the attribute was added to the rule. If the ratio of the two largest SDR measures among all potential attributes exceeds a threshold, the feature with the largest SDR is added to the rule to expand it. When an example is received, it is used to update the statistics to compute the SDR values of the first rule that covers it, if the ruleset is ordered, or of all the rules that cover it, if the set is unordered. Expansion of a rule is only considered after it has received a certain minimum number of examples N _min .

Rule creation. If the default rule is expanded, it will become a normal rule and will be added to the model’s ruleset. A new default rule is initialized to replace the expanded one.

Rule deletion. The error rate of every rule on the examples that it covers is monitored with a Page-Hinkley test. If the test indicates that its cumulative error exceeds a threshold, then the rule may be removed.

AMRules is reported in [ 90 , 92 ] to have better performance on average than IBLStreams and FIMT-DD on a variety of synthetic and real datasets. The unordered version seems to achieve a slightly lower error rate than the ordered version; however, this is at the cost of interpretability, because the prediction for an example is easier to understand if it comes from a single rule than if it is the average of several rules.

8.7 Regression in MOA

MOA currently includes the algorithms discussed in this chapter: the Average (or Majority) algorithm, the Perceptron, IBLStreams (as an extension), and AMRules.

It also includes SGD, a stochastic gradient descent for learning various linear models (binary class SVM, binary class logistic regression and linear regression), and SPegasos, the stochastic variant of the Pegasos (Primal Estimated sub-GrAdient SOlver for SVM) method of Shalev-Shwartz et al. [ 226 ].